EM算法
Jensen不等式
EM算法
EM(expectation maximization)算法是一种迭代算法,用于含有隐藏变量的概率模型参数的极大似然估计;EM算法的每次迭代由两步组成:E步是求期望(Q函数),M步是极大化;E步估计隐含变量,M步估计其他参数。
用Y表示观测随机变量的数据,Z表示隐藏随机变量的数据;Y和Z连在一起称为完全数据,观测数据Y又称为不完全数据。
Q函数:完全数据的对数似然函数关于在给定观测数据和当前参数下对未观测数据的条件概率分布的期望称为Q函数.
给定训练样本,样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
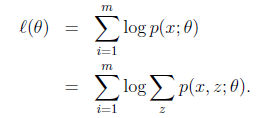
第一步是对极大似然取对数,第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求theta一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化l(theta),我们可以不断地建立l(theta)的下界(E步),然后优化下界(M步)。
对于每一个样例i,让Qi表示该样例隐含变量z的某种分布。(1)到(2)比较直接,就是分子分母同乘以一个相等的函数。(2)到(3)利用了Jensen不等式。
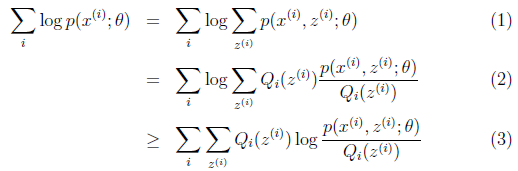
(3)步可以看作是对l(theta)求了下界。如果theta已经给定,那么我们可以不断调整Qi和p来逼近l(theta)的真实值。y
固定其他参数theta之后,Qi的计算公式如下。它是个后验概率,这一步就是E步,建立l(theta)的下界。
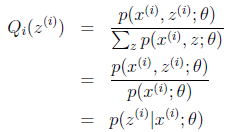
接下来M步,就是在给定Qi之后,调整theta,极大化l(theta)的下界。
我们不断的重复E步和M步,直到收敛。一种收敛方法是l(theta)不再变化,还有一种就是变化幅度很小。
高斯混合模型
高斯混合模型
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。
参数:混合系数;每个高斯分布的期望、方差
E步
求Qi:
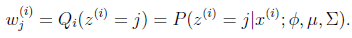
M步
固定Qi后最大化似然估计:

得到:
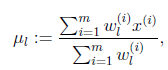
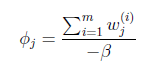
总结
如果将样本看作观察值,潜在类别看作是隐藏变量,那么聚类问题也就是参数估计问题,只不过聚类问题中参数分为隐含类别变量和其他参数,这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM上,E步估计隐含变量,M步估计其他参数,交替将极值推向最大。EM中还有“硬”指定和“软”指定的概念,“软”指定看似更为合理,但计算量要大,“硬”指定在某些场合如K-means中更为实用(要是保持一个样本点到其他所有中心的概率,就会很麻烦)。
EM的收敛性证明方法,利用log的凹函数性质,并且利用创造下界,拉平函数下界,优化下界的方法来逐步逼近极大值。而且每一步迭代都能保证是单调的。最重要的是证明的数学公式非常精妙,硬是分子分母都乘以z的概率变成期望来套上Jensen不等式。
在Mitchell的Machine Learning书中也举了一个EM应用的例子,明白地说就是将班上学生的身高都放在一起,要求聚成两个类。这些身高可以看作是男生身高的高斯分布和女生身高的高斯分布组成。因此变成了如何估计每个样例是男生还是女生,然后在确定男女生情况下,如何估计均值和方差,里面也给出了公式,有兴趣可以参考。