模型融合

介绍

模型融合被分为两个步骤：

产生一系列的base learners，可以通过parallel style或者sequential style的方式生成。
base learners通过策略结合成一个分类器。
bagging(并行+少方差)
boosting（串行+少偏差)
stacking（输出–>输入）

Voting

假设对于一个二分类问题，有3个基础模型，那么就采取投票制的方法，投票多者确定为最终的分类。

Averaging

对于回归问题，一个简单直接的思路是取平均。稍稍改进的方法是进行加权平均。权值可以用排序的方法确定，举个例子，比如A、B、C三种基本模型，模型效果进行排名，假设排名分别是1，2，3，那么给这三个模型赋予的权值分别是3/6、2/6、1/6。

这两种方法看似简单，其实后面的高级算法也可以说是基于此而产生的，Bagging或者Boosting都是一种把许多弱分类器这样融合成强分类器的思想。

Bagging

Bagging就是采用有放回的方式进行抽样，用抽样的样本建立子模型，对子模型进行训练，这个过程重复多次，最后进行融合。大概分为这样两步：

重复K次。有放回地重复抽样建模，训练子模型。
模型融合。分类问题：voting；回归问题：average。

Bagging算法不用我们自己实现，随机森林就是基于Bagging算法的一个典型例子，采用的基分类器是决策树。R和python都集成好了，直接调用。

随机森林

主要包括两个方面：

数据的随机性选取
待选特征的随机选取

通过样本随机和特征集随机来提升模型的鲁棒性。这个模型的优势在于它很难过拟合，可以放心大胆的迭代下去。不好的地方则是随机的可解释性，你的效果比别人好，到底是模型好还是运气好。

调参

RF需要调参的参数也包括两部分，第一部分是Bagging框架的参数，第二部分是CART决策树的参数。

RF框架参数：RF重要的框架参数比较少，主要需要关注的是n_estimators，即RF最大的决策树个数。

n_estimators：也就是弱学习器的最大迭代次数，或者说最大的弱学习器的个数。
oob_score：即是否采用袋外样本来评估模型的好坏。默认识False。个人推荐设置为True，因为袋外分数反应了一个模型拟合后的泛化能力。
criterion：即CART树做划分时对特征的评价标准。分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini，另一个可选择的标准是信息增益。回归RF对应的CART回归树默认是均方差mse，另一个可以选择的标准是绝对值差mae。一般来说选择默认的标准就已经很好的。

RF决策树参数：决策树参数中最重要的包括最大特征数max_features，最大深度max_depth，内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf。

max_features：RF划分时考虑的最大特征数。
max_depth：决策树最大深度。
min_samples_split：内部节点再划分所需最小样本数。
min_samples_leaf：叶子节点最少样本数。
min_weight_fraction_leaf：叶子节点最小的样本权重和。
max_leaf_nodes：最大叶子节点数。
min_impurity_split：节点划分最小不纯度。

首先对n_estimators进行网格搜索；我们得到了最佳的弱学习器迭代次数，接着我们对决策树最大深度max_depth和内部节点再划分所需最小样本数min_samples_split进行网格搜索（对于内部节点再划分所需最小样本数min_samples_split，我们暂时不能一起定下来，因为这个还和决策树其他的参数存在关联）；下面我们再对内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf一起调参；最后我们再对最大特征数max_features做调参。

Boosting

boosting的每一次抽样的样本分布都是不一样的。每一次迭代，都根据上一次迭代的结果，增加被错误分类的样本的权重，使得模型能在之后的迭代中更加注意到难以分类的样本，这是一个不断学习的过程，也是一个不断提升的过程，这也就是boosting思想的本质所在。

Bagging算法可以并行处理，而Boosting的思想是一种迭代的方法，每一次训练的时候都更加关心分类错误的样例，给这些分类错误的样例增加更大的权重，下一次迭代的目标就是能够更容易辨别出上一轮分类错误的样例。最终将这些弱分类器进行加权相加。

同样地，基于Boosting思想的有AdaBoost、GBDT等，在R和python也都是集成好了直接调用。

Boosting模型是采用加法模型（即基函数的线性组合）与前向分布算法。以决策树为基函数的提升方法称为提升树（boosting tree）。（统计学习三要素：模型、策略和算法）

Adaboost算法是模型为加法模型，损失函数为指数函数，学习算法为前向分布算法的二类分类学习方法。

GBDT回归算法是模型为加法模型，损失函数为平方误差，学习算法为前向分布算法的学习方法。

上述平方损失和指数损失每一步优化很简单，但对于其他损失函数可能优化不是很容易，所以提出了梯度提升算法（gradient boosting），利用最速下降法的近似方法，关键是利用损失函数的负梯度来拟合。

不同的损失函数和极小化损失函数方法决定了boosting的最终效果

从损失函数谈一谈adaboost和GBDT和xgboost的区别

Adaboost和GBDT都属于boosting提升方法，AdaBoost是通过提升错分数据点的权重来定位模型的不足，而Gradient Boosting是通过计算负梯度来定位模型的不足。

从损失函数谈一谈adaboost和GBDT和xgboost的区别

adaboost和gradient boost不同的地方在于，adaboost不需要求梯度。那么adaboost模型为什么还会有learning rate？

AdaBoost

Input: Data set D = {(x1, y1), (x2, y2), · · · , (xm, ym)}; 
       Base learning algorithm L;
       Number of learning rounds T .
Process:
  D1(i) = 1/m. % Initialize the weight distribution
  for t = 1,··· ,T:
    ht = L(D, Dt ); % Train a base learner ht from D using distribution Dt
    εt = Pri∼D [ht(xi ̸= yi)]; % Measure the error of ht
    αt % Determine the weight of ht exp(−αt) if ht(xi) = yi
    Dt+1(i) % Update the distribution
end.
Output: H(x) = sign (f (x)) = sign (from t=1 to T, add αtht(x))

关键字：样本的权重分布。

为了防止Adaboost过拟合，我们通常也会加入正则化项，这个正则化项我们通常称为步长(learning rate)。

调参

当我们对Adaboost调参时，主要要对两部分内容进行调参，第一部分是对我们的Adaboost的框架进行调参，第二部分是对我们选择的弱分类器进行调参。两者相辅相成。

AdaBoostClassifier和AdaBoostRegressor框架参数：

base_estimator：弱分类学习器或者弱回归学习器。默认是决策树，即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier，而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor。
algorithm：这个参数只有AdaBoostClassifier有。主要原因是scikit-learn实现了两种Adaboost分类算法，SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量，SAMME用对样本集分类效果作为弱学习器权重，而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值，迭代一般比SAMME快，因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了，但是要注意的是使用了SAMME.R，则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。
loss：这个参数只有AdaBoostRegressor有，Adaboost.R2算法需要用到。有线性‘linear’, 平方‘square’和指数‘exponential’三种选择，默认是线性，一般使用线性就足够了，除非你怀疑这个参数导致拟合程度不好。
n_estimators：弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。默认是50。在实际调参的过程中，我们常常将n_estimators和下面介绍的参数learning_rate一起考虑。
learning_rate: AdaBoostClassifier和AdaBoostRegressor都有，即每个弱学习器的权重缩减系数ν，在原理篇的正则化章节我们也讲到了，加上了正则化项，我们的强学习器的迭代公式为fk(x)=fk−1(x)+ναkGk(x)。ν的取值范围为0<ν≤1。对于同样的训练集拟合效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。所以这两个参数n_estimators和learning_rate要一起调参。一般来说，可以从一个小一点的ν开始调参，默认是1。

AdaBoostClassifier和AdaBoostRegressor弱学习器参数：

max_features：划分时考虑的最大特征数。默认是”None”,意味着划分时考虑所有的特征数；如果是”log2”意味着划分时最多考虑log2N个特征；如果是”sqrt”或者”auto”意味着划分时最多考虑根号N个特征。如果是整数，代表考虑的特征绝对数。如果是浮点数，代表考虑特征百分比，即考虑（百分比xN）取整后的特征数。其中N为样本总特征数。一般来说，如果样本特征数不多，比如小于50，我们用默认的”None”就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
max_depth：决策树最大深度。如果不输入的话，决策树在建立子树的时候不会限制子树的深度。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
min_samples_split：内部节点再划分所需最小样本数。这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
min_samples_leaf：叶子节点最少样本数。这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
min_weight_fraction_leaf：叶子节点最小的样本权重。这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
max_leaf_nodes：最大叶子节点数。通过限制最大叶子节点数，可以防止过拟合，默认是”None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。

GBDT

AdaBoost是Gradient Boosting的一个特例或者Gradient Boosting是对AdaBoosting进行推广。模型的训练过程是对一任意可导目标函数的优化过程。因此可以说Gradient Boosting = Gradient Descent + Boosting。

和Adaboost一样，Gradient Boosting也是重复选择一个表现一般的模型并且每次基于先前的模型表现进行调整。不同的是，Adaboost是通过提升错分数据点的权重来定位模型的不足而Gradient Boosting是通过算梯度（gradient）来定位模型的不足。因此，相比Adaboost，Gradient Boosting可以使用更多种类的目标函数。

GBDT是以决策树（CART）为基学习器的GB算法，是回归树，而不是分类树。Boost是”提升”的意思，一般Boosting算法都是一个迭代的过程，每一次新的训练都是为了改进上一次的结果。有了前面Adaboost的铺垫，大家应该能很容易理解大体思想。

GBDT的训练过程：

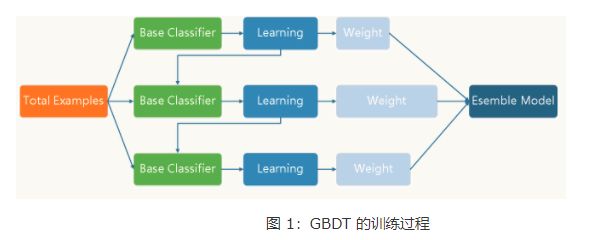
GBDT的核心就在于：每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学习。

GBDT主要由三个概念组成：Regression Decistion Tree（即DT)，Gradient Boosting（即 GB)，Shrinkage。

GBDT的并行以及后来出现的Xgboost的并行主要是针对单棵树特征处理和选择的并行（特征排序），以及在模型完成后进行预测时的并行。

gbdt并行?

gbdt正则化?

GBDT的正则化

Regression Decistion Tree

GBDT中的树都是回归树，不是分类树。

Gradient Boosting

每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。

Shrinkage

Shrinkage（缩减）的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。用方程来看更清晰，即：

没用Shrinkage时：（yi表示第i棵树上y的预测值， y(1~i)表示前i棵树y的综合预测值）

y(i+1) = 残差(y1~yi)，其中：残差(y1~yi) = y真实值 - y(1 ~ i)

y(1 ~ i) = SUM(y1, …, yi)

Shrinkage不改变第一个方程，只把第二个方程改为：

y(1 ~ i) = y(1 ~ i-1) + step * yi

即Shrinkage仍然以残差作为学习目标，但对于残差学习出来的结果，只累加一小部分（step*残差）逐步逼近目标，step一般都比较小，如 0.01~0.001（注意该step非gradient的step），导致各个树的残差是渐变的而不是陡变的。直觉上这也很好理解，不像直接用残差一步修复误差，而是只修复一点点，其实就是把大步切成了很多小步。本质上，Shrinkage为每棵树设置了一个weight，累加时要乘以这个weight，但和Gradient并没有关系。这个weight就是step。就像Adaboost一样，Shrinkage能减少过拟合发生也是经验证明的，目前还没有看到从理论的证明。

Xgboost（eXtreme Gradient Boosting）

Gradient Boosting Machine的一个C++实现。它可以自动利用CPU的多线程进行并行，同时在算法上改进提高了精度。

xgboost提高效率的优化：

借助OpenMP,自动利用CPU的多核进行并行计算。
定义了一个数据矩阵类DMatrix，会在训练开始时进行一遍预处理，从而提高之后每次迭代的效率。
准确度提升的原因：和传统的GBDT相比加入了对于模型复杂度的控制以及后期的剪枝处理，使学习出来的模型更加不容易过拟合。

Xgboost相比于GBDT来说，更加有效应用了数值优化，最重要是对损失函数（预测值和真实值的误差）变得更复杂。目标函数依然是所有树的预测值相加等于预测值。

损失函数如下，引入了一阶导数，二阶导数。

好的模型需要具备两个基本要素：一是要有好的精度（即好的拟合程度），二是模型要尽可能的简单（复杂的模型容易出现过拟合，并且更加不稳定）。因此，如上图所示，我们构建的目标函数右边第一项是模型的误差项，第二项是正则化项（也就是模型复杂度的惩罚项）。

常用的误差项有平方误差和逻辑斯蒂误差，常见的惩罚项有l1，l2正则，l1正则是将模型各个元素进行求和，l2正则是对元素求平方。

分裂算法

类似于随机森林，XGBoost在构建树的过程中，对每棵树随机选择一些属性作为分裂属性。

分裂算法有两种，一种是精确的分裂，一种是近似分裂算法。

精确分裂算法就是把每个属性的每个取值都当作一次阈值进行遍历，采用的决策树是CART。值得注意的是，由于要遍历所有的属性的所有取值，因此，通常需要在训练之前对所有样本做一个预排序(pre-sort)，从而避免每次选择属性都要重新排序。

近似分裂算法：对于值为连续值的特征，当样本数非常大时，该特征取值过多，遍历所有取值复杂度较高，而且容易过拟合。因此，考虑将特征值分桶，即找到l个分位点，将位于相邻分位点之间的样本分在一个桶中，在遍历该特征的时候，只需要遍历各个分位点，从而计算最优划分。注意到上面算法流程中说明了有全局的近似(global)和局部的近似(local)，所谓全局就是在新生成一棵树之前就对各个特征计算分位点并划分样本，之后在每次分裂过程中都采用近似划分，而局部就是在具体的某一次分裂节点的过程中采用近似算法。

XGBoost提出了一个特殊的分桶策略，一般的分桶策略是每个样本的权重都是相同的，但是XGBoost使每个样本的权重为损失函数在该样本点的二阶导数。

对稀疏数据的支持

XGBoost添加了对稀疏数据的支持，在计算分裂收益的时候只利用没有missing值的那些样本，但是在推理的时候，也就是在确定了树的结构，需要将样本映射到叶子节点的时候，需要对含有缺失值的样本进行划分，XGBoost分别假设该样本属于左子树和右子树，比较两者分裂增益，选择增益较大的那一边作为该样本的分裂方向。

XGBOOST相比于GBDT有何不同？XGBOOST为什么快？XGBOOST如何支持并行？

GBDT只能用CART回归树，而XGBOOST可以用CART树（回归/分类），还可以用用想LR之类的线性模型，相当于加入L1、L2正则项的LR或线性回归。
列抽样，可以并行，不是树粒度上的，是特征粒度上的，block块，并行计算所有信息增益等信息。
可处理多种特征，且对缺失值也不用进行处理。
GBDT在残差梯度下降方向拟合，一阶导；XGBOOST泰勒展开至二阶导。
近似直方图算法，高效生产候选分割点。
shrink，缩减，叶子节点同时乘，防止过拟合。
可以自己定义评价函数。
代价函数含正则化项，防止过拟合。
xgboost算法都认为是gbdt的一种变体。但是与传统的gbdt不同，它并不是先求出N个点的一阶导数（或者二阶导数，类似优化中的Newton step），然后用tree来拟合这N个导数值。相反，xgboost把叶子节点的数值(weight)直接代入到了代价函数的二阶展开近似中进行优化，所以它的叶子节点值是由优化函数来决定的。而传统的regression tree最终的叶子节点值，一般取位于此叶子的数据节点的平均值。两者并不相同。猜测xgboost这种直接来优化目标函数的方式要比gbdt的间接方式更高效。
剪枝：GBDT是ccp剪枝；https://www.zhihu.com/question/41354392 回答中“当增益大于阈值时才让节点分裂，上式中的gamma即阈值，它是正则项里叶子节点数T的系数，所以xgboost在优化目标函数的同时相当于做了预剪枝”，但根据XGBoost另一合作者Tong He的slides http://www.saedsayad.com/docs/xgboost.pdf，似乎有所矛盾。从上述slides中第84页，可以看到并没有根据gain的正负来进行预剪枝。相反，无论gain正负，XGBoost都会选择最大gain所对应的特征及数值点来进行分割，直到用户指定的max_depth。之后有个prune的过程，即将负值gain相关的叶子节点去掉。个人也没想明白为什么要这样做，有点多此一举的感觉。可能这是一种探索，即当前叶子节点gain为负，但分裂后的左右分支如果再分裂可能得到gain为正。相关slides是2015年的，也许当前的版本已经做了变动。(有人发表的这种做法的优点，当一个负损失（如-2）后面有个正损失（如+10）的时候，就显现出来了。GBM会在-2处停下来，因为它遇到了一个负值。但是XGBoost会继续分裂，然后发现这两个分裂综合起来会得到+8，因此会保留这两个分裂。)
w是最优化求出来的，考虑到了一阶导、二阶导、正则化；回归问题中gbdt中的w是平均值，在回归问题中是通过最小化均方误差得到的这个结果。

本质问题：

GBDT采用的是数值优化的思维，用的最速下降法去求解Loss Function的最优解，其中用CART决策树去拟合负梯度，用牛顿法求步长。XGboost用的解析的思维，对Loss Function展开到二阶近似，求得解析解，用解析解作为Gain来建立决策树，使得Loss Function最优.

Xgboost和深度学习的关系

不同的机器学习模型适用于不同类型的任务。深度神经网络通过对时空位置建模，能够很好地捕获图像、语音、文本等高维数据。而基于树模型的XGBoost则能很好地处理表格数据，同时还拥有一些深度神经网络所没有的特性（如：模型的可解释性、输入数据的不变性、更易于调参等）。

这两类模型都很重要，并广泛用于数据科学竞赛和工业界。举例来说，几乎所有采用机器学习技术的公司都在使用tree boosting，同时XGBoost已经给业界带来了很大的影响。

RF与传统bagging的区别

样本采样：RF有放回选取和整体样本数目相同的样本，一般bagging用的样本<总体样本数。
特征采样：RF对特征进行采样，bagging用全部特征

Stacking

融合多个强分类器。

Stacking模型本质上是一种分层的结构。

首先，在我看来stacking严格来说不能称为一种算法，我理解的是一种非常精美而复杂的对模型的集成策略。大家都知道，在给定了数据集的情况下，数据内部的空间结构和数据之间的关系是非常复杂的。而不同的模型，其实很重要的一点就是在不同的角度去观测我们的数据集。举个例子，KNN可能更加关注样本点之间的距离关系（包括欧几里得距离（Euclidean Distance）、明可夫斯基距离（Minkowski Distance等等），当样本距离相对较近，KNN就把他们分为一类；而决策树，可能更加关注分裂节点时候的不纯度变化，有点像我们自己找的规则，在满足某个条件且满足某个条件的情况下，决策树把样本分为一类等等。也就是说，不同的算法模型，其实是在不同的数据空间角度和数据结构角度来观测数据，然后再依据它自己的观测，结合自己的算法原理，来建立一个模型，在新的数据集上再进行预测。既然是不同的算法对数据有不同的观测，那么我们能不能相互取长补短，我看看你的观测角度，你看看我的观测角度，咱俩结合一下，是不是可以得到一个更加全面更加优秀的结果呢？答案是肯定的。

一些理解：

Stacking是一种表示学习(representation learning)。表示学习指的是模型从原始数据中自动抽取有效特征的过程，比如深度学习就是一种表示学习的方法。
Stacking和神经网络从某种角度看有异曲同工之妙，神经网络也可以被看作是集成学习。stacking的学习能力主要来自于对于特征的表示学习，这和神经网络的思路是一致的。而且神经网络也可以被看做是一种集成学习，主要取决于不同神经元、层对于不同特征的理解不同。从浅层到深层可以理解为一种从具体到抽象的过程。Stacking中的第一层可以等价于神经网络中的前 n-1层，而stacking中的最终分类层可以类比于神经网络中最后的输出层。不同点在于，stacking中不同的分类器通过异质来体现对于不同特征的表示，神经网络是从同质到异质的过程且有分布式表示的特点(distributed representation)。Stacking中应该也有分布式的特点，主要表现在多个分类器的结果并非完全不同，而有很大程度的相同之处。stacking集成学习框架的对于基分类器的两个要求：差异化(diversity)要大、准确性(accuracy)要高。
为了降低过拟合的问题，第二层分类器应该是较为简单的分类器，广义线性如逻辑回归是一个不错的选择。在特征提取的过程中，我们已经使用了复杂的非线性变换，因此在输出层不需要复杂的分类器。这一点可以对比神经网络的激活函数或者输出层，都是很简单的函数，一点原因就是不需要复杂函数并能控制复杂度。
一般来看，2层对于stacking足够了。多层的stacking会面临更加复杂的过拟合问题，且收益有限。第一层分类器的数量对于特征学习应该有所帮助，经验角度看越多的基分类器越好。即使有所重复和高依赖性，我们依然可以通过特征选择来处理，问题不大。

一些注意事项：

stacking的框架设计比较复杂，对于一个基模型要训练5次，如果你的一个xgb模型要训练2个小时，即使在进行stacking的时候每折减少了五分之一的数据量，你的计算时间仍然是很可观的。所以建议在使用的时候要计算时间的耗费，或者可以改为3折，4折等等。
基模型除了是不同参数的相同模型之外，比如不同参数的xgboost，或者不同K值的KNN等等；更重要的是要尽可能的多加一些不同种类的基模型进去，也就是说所谓的模型要“跨越空间”的概念。这样的话我们的集成结果会更加稳健，更加精确。

stacking的一些基本变种改进：

在变种改进方面，我们可以不仅对模型进行融合，还可以对特征级进行一些变化，比如选部分特征做stacking；或者对stacking的结果进行再次的stacking，我们上面介绍的是两层的stacking，可以有3层，或者更多。但是时间复杂度很高，效果并不一定明显。

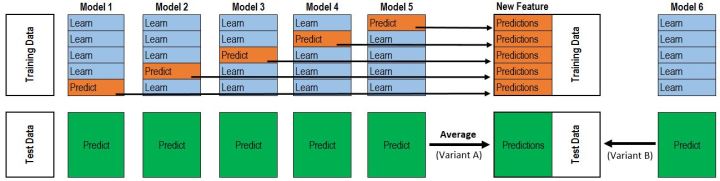
如下分析二级Stacking。第一层循环控制基模型的数目，每一个基模型要得到P1，T1，第二层循环控制的是交叉验证的次数K，对每一个基模型，会训练K次最后拼接得到P1，取平均得到T1。

下图是一个基模型得到P1和T1的过程，采用的是5折交叉验证，所以循环了5次，拼接得到P1，测试集预测了5次，取平均得到T1。而这仅仅只是第二层输入的一列/一个特征，并不是整个训练集。

关于Boosting和Bagging

通常来说boosting是在优化loss function，在降低loss，那么很显然，这在很大程度上是减少bias。而bagging，之所以进行bagging，是希望模型能够具有更好的鲁棒性，也就是稳定性，希望避免过拟合，显然这就是在减少variance。
Boosting针对每个弱模型进行训练，按照序列方式进行，每次训练都挑出上一次未训练好的样例，再进行训练。最终提升模型在训练集上的准确度，减小bias。
decision + bagging其实做了两个事情减少了variance。第一，bootstrap；就是从training data里面sample with replacement，然后生成training data x N。第二，averaging from all the output。
random forest其实是bagging的延伸。除了bootstrap还加的idea就是每次build tree的时候只选一部分的attribute，因为decision tree一般很受重要的attribute的影响。