概述
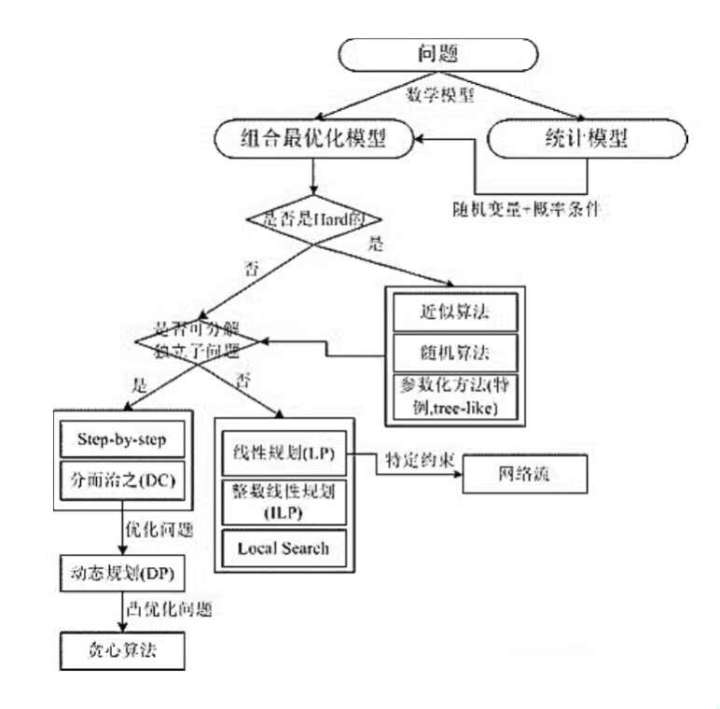
分治法:对于组合最优化模型,考虑是否可分成独立子问题。如果可以则可以考虑将问题分成更小的子问题,分别进行处理后再将小问题的解合并起来得到大问题的解。
动态规划:动态规划与分治法非常像,都是要把大问题分解,然后再将小问题的解合并起来得到大问题的解。但动态规划一般会首先枚举所有的子问题,把所有子问题都解决一遍,通过生成一张记录子问题的表来减少重复计算、大大降低复杂度。动态规划要求最优子结构。
某种程度下,动态规划是贪心算法的泛化,而贪心算法是动态规划的特例。
分治法
分治法能解决的问题具有的特征:
- 该问题的规模缩小到一定程度就可以容易地解决。
- 该问题可以分为若干个较小规模的相似的问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的且子问题之间不包含公共的子问题。
上述的第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加。第二条特征是分治法应用的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用。
第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑贪心算法或动态规划算法。
第四条特征涉及到分治法的效率,如果各个子问题不是独立的,则分治法要做许多不必要的工作,重复地解公共的子问题。这类问题虽然可以用分治法解决,但用动态规划算法解决效率更高。
当问题满足第一、二、三条,而不满足第四条时,一般可以用动态规划法解决,可以说,动态规划法的实质是:分治算法思想 + 解决子问题冗余情况。
动态规划
动态规划能解决的问题具有的特征:
- 最优子结构性质。
- 有重叠子问题。
一般来说,给定一个规则,让我们求任意状态下的解,都是用动态规划。
示例:打家劫舍
贪心算法
贪心算法能解决的问题具有的特征:
- 贪心选择性质。在求解一个问题的过程中,如果在每一个阶段的选择都是当前状态下的最优选择,即局部最优选择,并且最终能够求得问题的整体最优解,那么说明这个问题可以通过贪心选择来求解,这时就说明此问题具有贪心选择性质。
- 最优子结构性质:一个问题的最优解包含了这个问题的子问题的最优解。